上溢和下溢
连续数学在数字计算机上的根本困难是,我们需要通过有限数量的位模式来表示无限多的实数。这意味着我们在计算机中表示实数时,几乎总会引入一些近似误差。
种极具毁灭性的舍人误差是下溢( underflow)。当接近零的数被四舍五入为零时发生下溢。
另一个极具破坏力的数值错误形式是上溢( overfow)。当大量级的数被近似为+∞或-∞时发生上溢。进一步的运算通常会导致这些无限值变为非数字。
必须对上溢和下溢进行数值稳定的一个例子是softmax函数。
病态条件
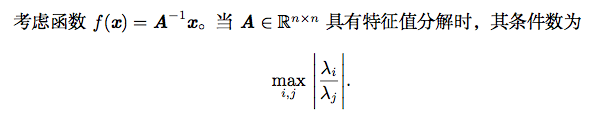
这是最大和最小特征值的模之比1 。当该数很大时,矩阵求逆对输入的误差特别敏感。
这种敏感性是矩阵本身的固有特性,而不是矩阵求逆期间舍入误差的结果。
基于梯度的优化方法
大多数深度学习算法都涉及某种形式的优化。优化指的是改变 x 以最小化或最 大化某个函数 f(x) 的任务。我们通常以最小化 f(x) 指代大多数最优化问题。最大化可经由最小化算法最小化−f(x) 来实现。
我们把要最小化或最大化的函数称为 目标函数(objective function)或 准则 (criterion)。当我们对其进行最小化时,我们也把它称为 代价函数(cost function)、 损失函数(loss function)或 误差函数(error function)。

有些临界点既不是最小点也不是最大点。这些点被称为 鞍点(saddle point)。
最速下降法(method of steepest descent) 或 梯度下降(gradient descent)。
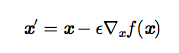
其中 ε 为 学习率(learning rate)。
梯度之上:Jacobian 和 Hessian 矩阵
有时我们需要计算输入和输出都为向量的函数的所有偏导数。包含所有这样的偏导数的矩阵被称为 Jacobian 矩阵。 雅可比矩阵。
当我们的函数具有多维输入时,二阶导数也有很多。我们可以将这些导数合并 成一个矩阵,称为 Hessian 矩阵。 黑塞矩阵。

Hessian 等价于梯度的 Jacobian 矩阵。

当 Hessian 的条件数很差时,梯度下降法也会表现得很差。
病态条件也导致很难选择合适的步长。步长必须足够小,以免冲过最小而向具有较强正曲率的方向上升。这通常意味着步长太小,以致于在其他较小曲率的方向上进展不明显。


牛顿法,
仅使用梯度信息的优化算法被称为一阶优化算法(first-order optimization al- gorithms),如梯度下降。使用 Hessian 矩阵的优化算法被称为二阶最优化算法(second-order optimization algorithms)(Nocedal and Wright, 2006),如牛顿法。
在深度学习的背景下,限制函数满足Lipschitz 连续(Lipschitz continuous)或 其导数Lipschitz连续可以获得一些保证。直觉上,利普希茨连续函数限制了函数改变的速度,符合利普希茨条件的函数的斜率,必小于一个称为利普希茨常数的实数(该常数依函数而定)。
最成功的特定优化领域或许是 凸优化(Convex optimization)。凸优化通过更强 的限制提供更多的保证。凸优化算法只对凸函数适用,即 Hessian 处处半正定的函 数。因为这些函数没有鞍点而且其所有局部极小点必然是全局最小点,所以表现很 好。然而,深度学习中的大多数问题都难以表示成凸优化的形式。凸优化仅用作一 些深度学习算法的子程序。凸优化中的分析思路对证明深度学习算法的收敛性非常 有用,然而一般来说,深度学习背景下凸优化的重要性大大减少。
约束优化
在 x 的某些集合 S 中找 f(x) 的最大值或最小值。这被称 为 约束优化(constrained optimization)。在约束优化术语中,集合 S 内的点 x 被称为可行(feasible)点。
我们常常希望找到在某种意义上小的解。针对这种情况下的常见方法是强加一 个范数约束,如 ||x|| ≤ 1。
Karush–Kuhn–Tucker(KKT)方法是针对约束优化非常通用的解决方案。KKT 方法是 Lagrange 乘子法(只允许等式约束)的推广。
我们可以使用一组简单的性质来描述约束优化问题的最优点。这些性质称 为 Karush–Kuhn–Tucker(KKT)条件 (Karush, 1939; Kuhn and Tucker, 1951)。 这些是确定一个点是最优点的必要条件,但不一定是充分条件。这些条件是:
- 广义 Lagrangian 的梯度为零。
- 所有关于 x 和 KKT 乘子的约束都满足。
- 不等式约束显示的 ‘‘互补松弛性’’.